📈
1
ตัวอย่าง
ง่าย
โจทย์
จงหาค่าของลิมิต
$$ \lim_{x \to 2} \frac{x^2 - 4}{x - 2} $$
วิธีคิด
เมื่อ $x \to 2$ จะได้รูป $\frac{0}{0}$ จึงต้องจัดรูปก่อน
$$x^2 - 4 = (x-2)(x+2)$$
ดังนั้น
$$\frac{x^2 - 4}{x - 2} = x + 2 \quad (\text{เมื่อ } x \neq 2)$$
$$\lim_{x \to 2}(x + 2) = 4$$
$$x^2 - 4 = (x-2)(x+2)$$
ดังนั้น
$$\frac{x^2 - 4}{x - 2} = x + 2 \quad (\text{เมื่อ } x \neq 2)$$
$$\lim_{x \to 2}(x + 2) = 4$$
คำตอบ:
ข้อ 3
—
4
2
ตัวอย่าง
ปานกลาง
โจทย์
กำหนดฟังก์ชัน f(x) = (x² − 1)/(x − 1) เมื่อ x ≠ 1 และ f(1) = a จงหาค่า a ที่ทำให้ f ต่อเนื่องที่ x = 1
$$ f(x) = \begin{cases} \frac{x^2 - 1}{x - 1} & x \neq 1 \\ a & x = 1 \end{cases} $$
วิธีคิด
เงื่อนไข "ต่อเนื่องที่ $x=1$" ต้องมี $\lim_{x \to 1} f(x) = f(1) = a$
จัดรูป:
$$\frac{x^2 - 1}{x - 1} = \frac{(x-1)(x+1)}{x-1} = x + 1 \quad (x \neq 1)$$
$$\lim_{x \to 1} f(x) = \lim_{x \to 1}(x+1) = 2$$
เพื่อให้ต่อเนื่อง ต้องกำหนด $a = 2$
จัดรูป:
$$\frac{x^2 - 1}{x - 1} = \frac{(x-1)(x+1)}{x-1} = x + 1 \quad (x \neq 1)$$
$$\lim_{x \to 1} f(x) = \lim_{x \to 1}(x+1) = 2$$
เพื่อให้ต่อเนื่อง ต้องกำหนด $a = 2$
คำตอบ:
ข้อ 3
—
2
3
ตัวอย่าง
ปานกลาง
โจทย์
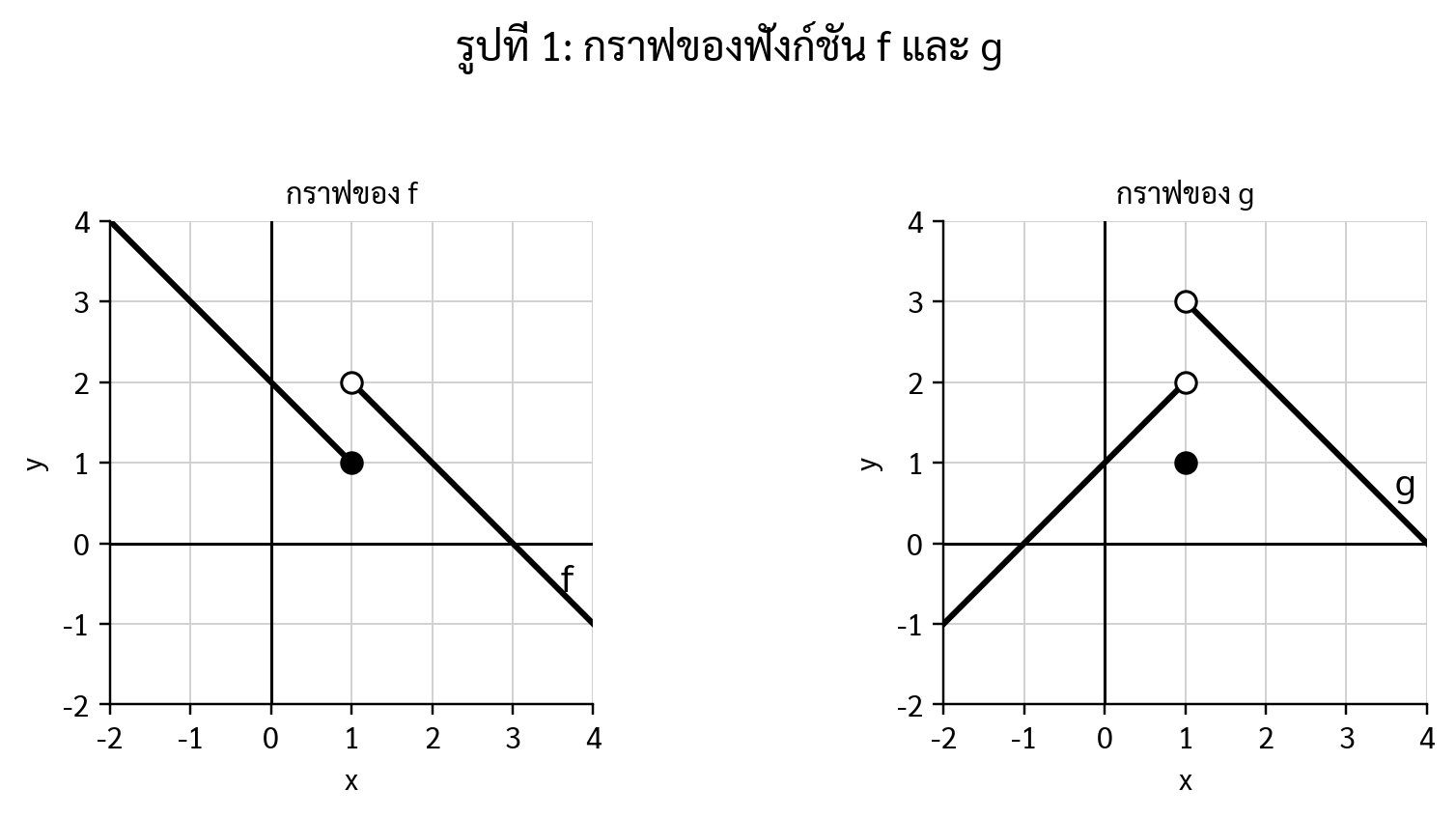
จากรูป จงหาค่าของลิมิตด้านซ้าย
$$ \lim_{x \to 1^{-}} \left( f(x) + g(x) \right) $$
วิธีคิด
ดูจากกราฟที่ $x$ เข้าใกล้ 1 "ทางซ้าย"
- กราฟ $f$ ทางซ้ายมีจุดทึบที่ $(1,1)$ ⇒ $\lim_{x \to 1^-} f(x) = 1$
- กราฟ $g$ ทางซ้ายเข้าใกล้วงกลมโปร่งที่ $(1,2)$ ⇒ $\lim_{x \to 1^-} g(x) = 2$
$$\lim_{x \to 1^-}\left(f(x) + g(x)\right) = 1 + 2 = 3$$
- กราฟ $f$ ทางซ้ายมีจุดทึบที่ $(1,1)$ ⇒ $\lim_{x \to 1^-} f(x) = 1$
- กราฟ $g$ ทางซ้ายเข้าใกล้วงกลมโปร่งที่ $(1,2)$ ⇒ $\lim_{x \to 1^-} g(x) = 2$
$$\lim_{x \to 1^-}\left(f(x) + g(x)\right) = 1 + 2 = 3$$
คำตอบ:
ข้อ 2
—
3
4
ตัวอย่าง
ปานกลาง
โจทย์
จากรูป ค่าของลิมิต (ถ้ามี) เท่ากับข้อใด
$$ \lim_{x \to 1} \left( f(x) + g(x) \right) $$

วิธีคิด
ต้องเทียบ "ลิมิตซ้าย" และ "ลิมิตขวา"
**ด้านซ้าย:** จากข้อก่อนหน้า $\lim_{x \to 1^-}(f+g) = 3$
**ด้านขวา:**
- $\lim_{x \to 1^+} f(x) = 2$ (ดูจากวงกลมโปร่ง)
- $\lim_{x \to 1^+} g(x) = 3$
$$\lim_{x \to 1^+}(f(x) + g(x)) = 2 + 3 = 5$$
เพราะ $3 \neq 5$ ⇒ ลิมิตสองข้างไม่เท่ากัน จึง **ไม่มีลิมิต**
**ด้านซ้าย:** จากข้อก่อนหน้า $\lim_{x \to 1^-}(f+g) = 3$
**ด้านขวา:**
- $\lim_{x \to 1^+} f(x) = 2$ (ดูจากวงกลมโปร่ง)
- $\lim_{x \to 1^+} g(x) = 3$
$$\lim_{x \to 1^+}(f(x) + g(x)) = 2 + 3 = 5$$
เพราะ $3 \neq 5$ ⇒ ลิมิตสองข้างไม่เท่ากัน จึง **ไม่มีลิมิต**
คำตอบ:
ข้อ 5
—
ไม่มีลิมิต
5
ตัวอย่าง
ยาก
โจทย์
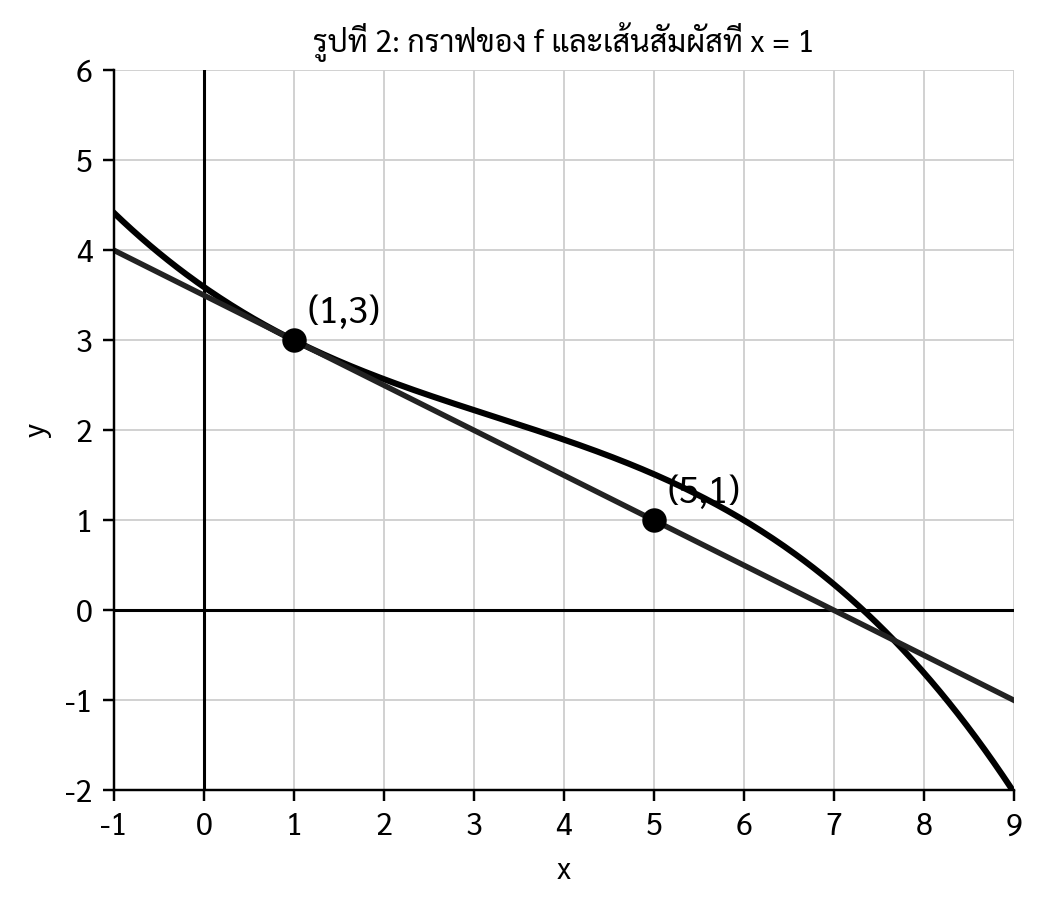
จากรูป กราฟของ f มีเส้นสัมผัสที่จุด (1,3) และเส้นสัมผัสนี้ผ่านจุด (5,1) จงหาค่า f'(1)
$$ f'(1) = ? $$
วิธีคิด
อนุพันธ์ที่จุด $x=1$ คือ "ความชันของเส้นสัมผัส" ที่จุดนั้น
$$m = \frac{y_2 - y_1}{x_2 - x_1}$$
ใช้จุด $(1,3)$ และ $(5,1)$:
$$m = \frac{1 - 3}{5 - 1} = \frac{-2}{4} = -\frac{1}{2}$$
ดังนั้น $f'(1) = -\frac{1}{2}$
$$m = \frac{y_2 - y_1}{x_2 - x_1}$$
ใช้จุด $(1,3)$ และ $(5,1)$:
$$m = \frac{1 - 3}{5 - 1} = \frac{-2}{4} = -\frac{1}{2}$$
ดังนั้น $f'(1) = -\frac{1}{2}$
คำตอบ:
ข้อ 3
—
$ -\frac{1}{2} $
อ่านตัวอย่างครบแล้ว พร้อมลองทำแบบฝึกหัดหรือยัง?