📈
1
ตัวอย่าง
ง่าย
โจทย์
จงหาค่าของอินทิกรัล
$$ \int_0^1 \frac{2x}{1 + x^2} \, dx $$
วิธีคิด
ให้ $u = 1 + x^2$ ⇒ $du = 2x \, dx$
เมื่อ $x = 0$ ⇒ $u = 1$
เมื่อ $x = 1$ ⇒ $u = 2$
$$\int_0^1 \frac{2x}{1 + x^2} \, dx = \int_1^2 \frac{1}{u} \, du = [\ln u]_1^2 = \ln 2 - \ln 1 = \ln 2$$
เมื่อ $x = 0$ ⇒ $u = 1$
เมื่อ $x = 1$ ⇒ $u = 2$
$$\int_0^1 \frac{2x}{1 + x^2} \, dx = \int_1^2 \frac{1}{u} \, du = [\ln u]_1^2 = \ln 2 - \ln 1 = \ln 2$$
คำตอบ:
ข้อ 1
—
$ \ln 2 $
2
ตัวอย่าง
ปานกลาง
โจทย์
จงหาค่าของอินทิกรัล
$$ \int_0^{\pi/2} \sin x \cos x \, dx $$
วิธีคิด
ใช้ $u = \sin x$ ⇒ $du = \cos x \, dx$
เมื่อ $x = 0$ ⇒ $u = 0$
เมื่อ $x = \frac{\pi}{2}$ ⇒ $u = 1$
$$\int_0^{\pi/2} \sin x \cos x \, dx = \int_0^1 u \, du = \left[\frac{u^2}{2}\right]_0^1 = \frac{1}{2}$$
เมื่อ $x = 0$ ⇒ $u = 0$
เมื่อ $x = \frac{\pi}{2}$ ⇒ $u = 1$
$$\int_0^{\pi/2} \sin x \cos x \, dx = \int_0^1 u \, du = \left[\frac{u^2}{2}\right]_0^1 = \frac{1}{2}$$
คำตอบ:
ข้อ 3
—
$ \frac{1}{2} $
3
ตัวอย่าง
ปานกลาง
โจทย์
ให้ F เป็นฟังก์ชันที่มีอนุพันธ์ และกำหนด F'(2x) = f(x + 2) โดยที่ F(0) = 4 และ F(2) = 10 จงหาค่าของอินทิกรัล
$$ \int_2^3 f(x) \, dx $$
วิธีคิด
จาก $F'(2x) = f(x+2)$
ให้ $x = u + 2$ ⇒ $u = x - 2$ และ $dx = du$
$$\int_2^3 f(x) \, dx = \int_0^1 f(u+2) \, du = \int_0^1 F'(2u) \, du$$
ให้ $v = 2u$ ⇒ $dv = 2du$ ⇒ $du = \frac{dv}{2}$
$$\int_0^1 F'(2u) \, du = \frac{1}{2} \int_0^2 F'(v) \, dv = \frac{1}{2}(F(2) - F(0)) = \frac{1}{2}(10 - 4) = 3$$
ให้ $x = u + 2$ ⇒ $u = x - 2$ และ $dx = du$
$$\int_2^3 f(x) \, dx = \int_0^1 f(u+2) \, du = \int_0^1 F'(2u) \, du$$
ให้ $v = 2u$ ⇒ $dv = 2du$ ⇒ $du = \frac{dv}{2}$
$$\int_0^1 F'(2u) \, du = \frac{1}{2} \int_0^2 F'(v) \, dv = \frac{1}{2}(F(2) - F(0)) = \frac{1}{2}(10 - 4) = 3$$
คำตอบ:
ข้อ 2
—
3
4
ตัวอย่าง
ปานกลาง
โจทย์
จากรูป พื้นที่ที่ล้อมด้วยกราฟ y = 2x และ y = x² ในช่วง x = 0 ถึง x = 2 มีค่าเท่ากับข้อใด
$$ \int_0^2 (2x - x^2) \, dx $$
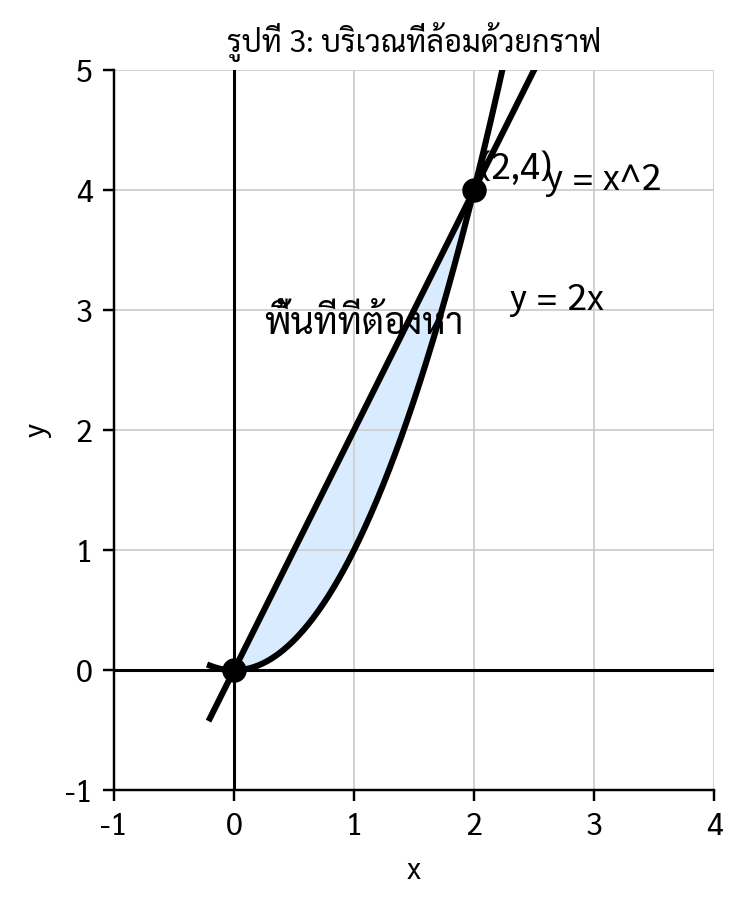
วิธีคิด
พื้นที่ระหว่างกราฟ = $\int (\text{กราฟบน} - \text{กราฟล่าง}) \, dx$
ในช่วง 0 ถึง 2: เส้นตรง $y = 2x$ อยู่เหนือพาราโบลา $y = x^2$
$$\text{พื้นที่} = \int_0^2 (2x - x^2) \, dx = \left[x^2 - \frac{x^3}{3}\right]_0^2$$
$$= \left(4 - \frac{8}{3}\right) - 0 = \frac{12 - 8}{3} = \frac{4}{3}$$
ในช่วง 0 ถึง 2: เส้นตรง $y = 2x$ อยู่เหนือพาราโบลา $y = x^2$
$$\text{พื้นที่} = \int_0^2 (2x - x^2) \, dx = \left[x^2 - \frac{x^3}{3}\right]_0^2$$
$$= \left(4 - \frac{8}{3}\right) - 0 = \frac{12 - 8}{3} = \frac{4}{3}$$
คำตอบ:
ข้อ 2
—
$ \frac{4}{3} $
5
ตัวอย่าง
ยาก
โจทย์
จงหาค่าของอินทิกรัล
$$ \int_0^1 x\sqrt{1 + x^2} \, dx $$
วิธีคิด
ให้ $u = 1 + x^2$ ⇒ $du = 2x \, dx$ ⇒ $x \, dx = \frac{du}{2}$
เมื่อ $x = 0$ ⇒ $u = 1$
เมื่อ $x = 1$ ⇒ $u = 2$
$$\int_0^1 x\sqrt{1 + x^2} \, dx = \int_1^2 \sqrt{u} \cdot \frac{du}{2} = \frac{1}{2} \int_1^2 u^{1/2} \, du$$
$$= \frac{1}{2} \cdot \left[\frac{2}{3}u^{3/2}\right]_1^2 = \frac{1}{3}(2^{3/2} - 1) = \frac{1}{3}(2\sqrt{2} - 1)$$
เมื่อ $x = 0$ ⇒ $u = 1$
เมื่อ $x = 1$ ⇒ $u = 2$
$$\int_0^1 x\sqrt{1 + x^2} \, dx = \int_1^2 \sqrt{u} \cdot \frac{du}{2} = \frac{1}{2} \int_1^2 u^{1/2} \, du$$
$$= \frac{1}{2} \cdot \left[\frac{2}{3}u^{3/2}\right]_1^2 = \frac{1}{3}(2^{3/2} - 1) = \frac{1}{3}(2\sqrt{2} - 1)$$
คำตอบ:
ข้อ 2
—
$ \frac{2\sqrt{2} - 1}{3} $
อ่านตัวอย่างครบแล้ว พร้อมลองทำแบบฝึกหัดหรือยัง?